Drawing Sierpinski triangle with Python

A few months ago I saw the following tweet

And because I have some free time on my hands now, I have decided to test whether it’s really true. I know that I could just look it up in wikipedia and believe it. But it is much more fun to try to “prove it”. So I wrote a quick script to draw it myself.

Step one:

Define a triangle. I want to have a bit of control over the shape of the triangle so I will initially define it as three constants, I will need the max resolution of my drawing and also number of points (calculation rounds) I am going to draw.

TRIANGLE = (coord((2000,1000), order='xy'),
coord((8000,900), order='xy'),
coord((500,8000), order='xy')
)
XMAX = 10000
YMAX = 10000
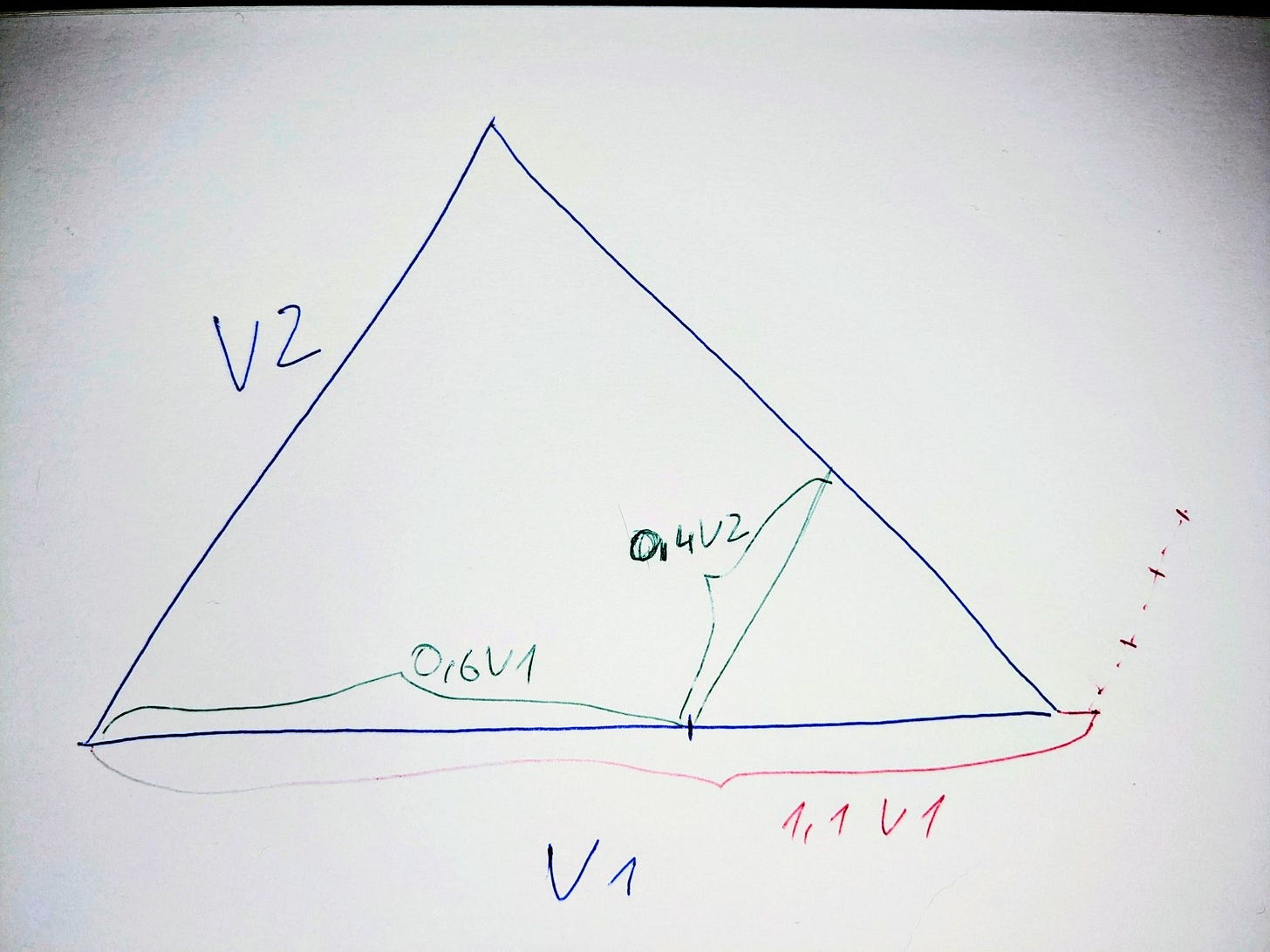
ROUNDS = 3000

Having the triangle ready I need to find a way to generate a random starting point within the triangle. I could use two sides of the triangle as vectors V1 and V2 and express any point within the triangle as a sum of the fractions of those vectors.

SP = a*V2 + b*V3

First rule:

0 < a, b < 1

From the picture it is quite clear that if I multiply V2 by a number greater than one I will end up passing the vertex T3 and by adding V3 multiplied by any number will never bring me inside the triangle. The same is true for V3 greater than 1.

Second rule :

Based on the similar triangles rule, all edges of the small triangle are in the same ratio to the edges of the big triangle, if all angles are equal. If we have a*V1 then b < 1-a which I can rewrite as

a + b < 1

and the code to find coordinates of a random point inside the triangle is:

def get_random_start(triangle) -> coord:
    """ Returns coordinates of a random point within the traingle.
    Args:
    triangle: A tuple of 3 coord of the vertices.
    Returns:
    coord of the point within the triangle.
    """
    t1, t2, t3 = triangle
    v2, v3 = t2 - t1, t3 - t1
    try_again = True
    while try_again:
        a = random.random()
        b = random.random()
    if a + b < 1:
        try_again = False
        new_coord = t1 + a * v2 + b * v3
    return new_coord

Good! I have a start and now I need to choose one of the three vertices and get the next point half distance from the previous point and the random vertex. Luckily the coordinates library has the vector math implemented so the code is very simple. Take random vertex, get the vector to the last point divide it by 2 and then add it to the last point to get the new point -something like this:

def get_next_point(triangle, last_coord) -> coord:
    """ Returns coordinates of the next point.
    Takes random vertex of the triangle and returns point
    half distance between last_coord and the vertex.
    Args:
    triangle: A tuple of 3 coord coordinates.
    last_coord: A coordinate of a point within the traingle.
    Returns:
    coord of the point half distance between
    last_coord and random vertex.
    """
    corner = triangle[random.randint(0,2)]
    new_coord = last_coord + (corner - last_coord)/2
    return new_coord

Now that I have all this out of the way, I can create a list of coordinates of all points in a simple loop.

def new_striangle():
    """ Returns all points of a Sierpinski triangle."""
    new_points = []
    new_points.extend(TRIANGLE)
    last_coord = get_random_start(TRIANGLE)
    for _ in range(ROUNDS):
        last_coord = get_next_point(TRIANGLE, last_coord)
        new_points.append(last_coord)
    return new_points

And the final step is to draw all points on the screen.

def init():
    ax.set_visible(False)
    ax.set_xlim(0, XMAX)
    ax.set_ylim(0, YMAX)
    return ln,


def update(crd):
    x_data.append(crd.x)
    y_data.append(crd.y)
    ln.set_data(x_data, y_data)
    return ln,


if __name__ == "__main__":
    random.seed()
    fig, ax = plt.subplots()
    x_data, y_data = [], []
    ln, = plt.plot([], [], 'ro', markersize=1)
    all_points = new_striangle()
    ani = FuncAnimation(fig, update, frames=all_points,
    init_func=init, interval=1, blit=True)
    plt.show()

I automatically went with matplotlib, and did not spend too much time poking around the animation. If anybody has any idea how to display the process better, let me know in the comments. For example by varying the delay between the point from slow to faster or displaying vertices and the start point different color and always on top.

Full code is here: https://github.com/michalpecek/sierpinski_triangle